After six years of graduate school – two at UMass-Amherst (MS, statistics), and four more at Brown University (PhD, biostatistics)…
On the thank you’s we never get to say
When I was 6, he was my babysitter who made peanut butter and jelly sandwiches and I cried because there…
The blog has moved!
To facilitate an easier sharing of code and figures, I’ve started a RMarkdown blog, which you will find at http://statsbylopez.netlify.com/. All…
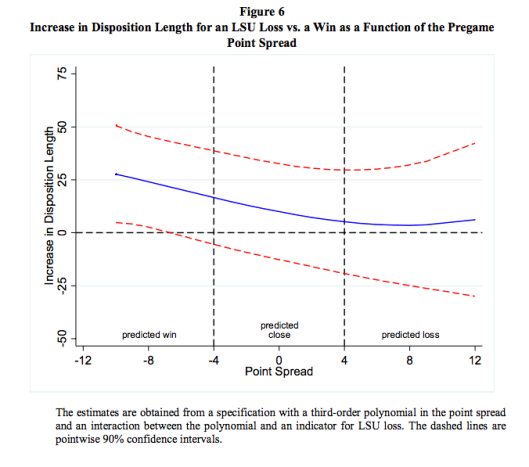
Triggered – a look at the LSU judge sentencing paper
One of the reasons I love the application of statistics to sports is the unique ways in which sports can…
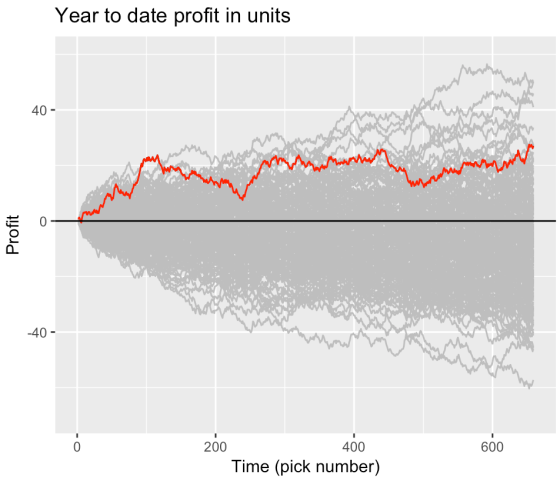
Evaluating sports predictions against the market
A few friends have been working on an algorithm for predicting baseball game outcomes. Roughly, the model uses player level…
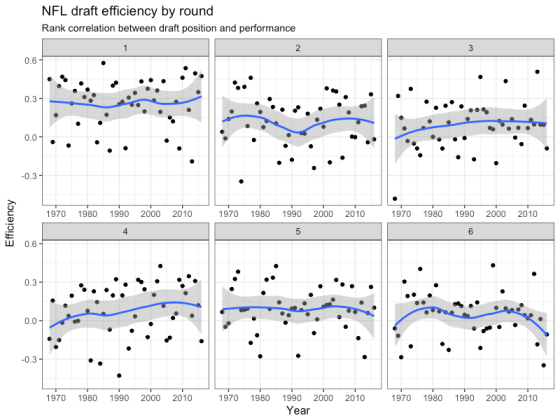
Evaluating the evaluators
Thursday’s NFL draft marks the culmination of several months — or perhaps years — of work. The amount of preparation that team scouts and…
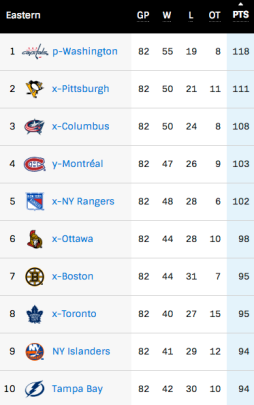
Nuts and bolts, the Metro Division got (a little bit) screwed
Here’s a look at the NHL’s final regular standings in the Eastern Conference from 2016-17. As a reminder, eight teams in…
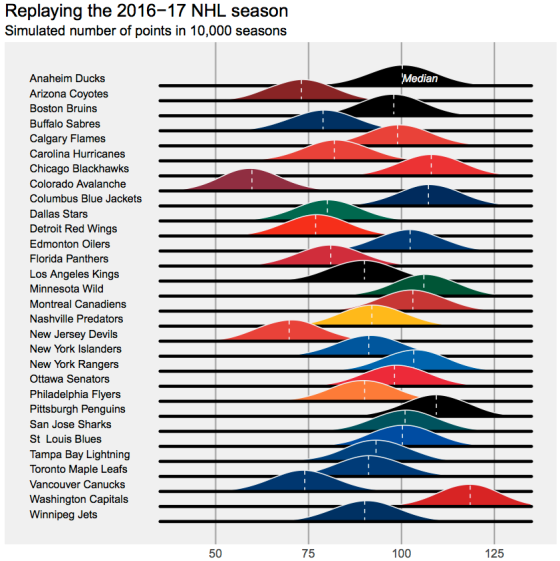
Towards an understanding of the NHL’s final standings
In a recent paper, Gregory Matthews, Ben Baumer, and I looked at the role of randomness in professional sports outcomes. Perhaps unsurprisingly,…
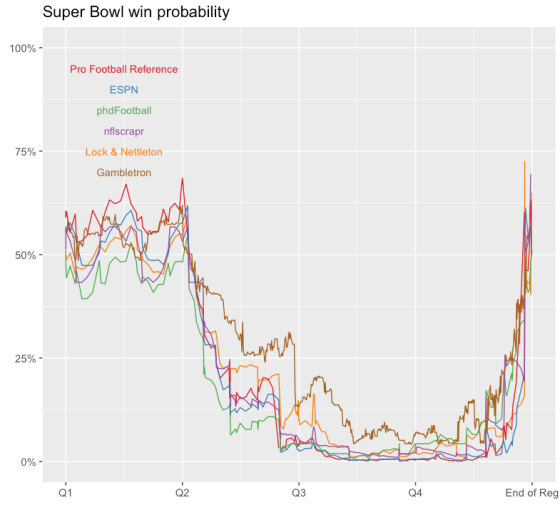
All win probability models are wrong — Some are useful
As in the moments following the 2016 US election, win probabilities took center stage in public discourse after New England’s comeback victory in…
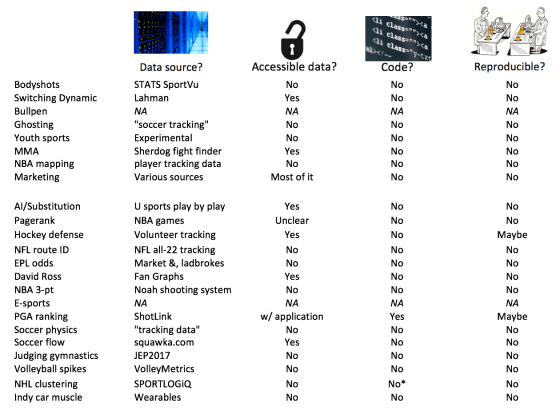
In Sloan’s paper contest, irreproducibility takes the stage
Over the last few years, researchers across fields have uncovered something that’s simultaneously humbling, frustrating, and scary: most research doesn’t…
Ref’s may respond to player aggression, too
Hockey die-hards like the sports’ reputation that the players police themselves. That is, teammates have one another’s backs, and acts of malice against…